Geometri Analitik: Konsep, Prinsip, dan Penerapannya

Geometri analitik adalah cabang matematika yang menggabungkan prinsip-prinsip aljabar dan geometri untuk menyelesaikan masalah-masalah geometris dengan menggunakan koordinat dan persamaan. Dengan menggunakan koordinat kartesian, kita dapat merepresentasikan objek-objek geometris seperti garis, lingkaran, parabola, dan hiperbola dalam bentuk persamaan matematika.

Ilustrasi sistem koordinat Kartesius yang digunakan dalam geometri analitik, menunjukkan hubungan antara titik koordinat dan objek geometris dalam ruang dua dimensi.

Dalam artikel ini, kita akan membahas konsep dasar geometri analitik, prinsip-prinsip yang terkait, dan beberapa contoh penerapannya dalam kehidupan sehari-hari.

Pengertian Geometri Analitik

Geometri analitik adalah studi tentang geometri menggunakan sistem koordinat dan prinsip-prinsip aljabar. Dalam sistem koordinat kartesian dua dimensi, setiap titik di bidang dapat dinyatakan sebagai pasangan terurut $(x, y)$ , di mana $x$ adalah jarak dari sumbu $y$ dan $y$ adalah jarak dari sumbu $x$ .

Konsep ini memungkinkan kita untuk:

Merepresentasikan bentuk geometris dalam persamaan aljabar.
Menggunakan teknik-teknik aljabar untuk menemukan solusi dari masalah geometris.
Mengkaji sifat-sifat dari objek geometris seperti panjang, jarak, kemiringan, dan luas.

Konsep Dasar dalam Geometri Analitik

Berikut beberapa konsep penting yang sering dipelajari dalam geometri analitik:

1. Sistem Koordinat Kartesian

Dalam sistem koordinat kartesian, sebuah titik di ruang dua dimensi dinyatakan dengan pasangan , di mana:

adalah nilai absis (jarak horizontal dari sumbu $y$ ).
adalah nilai ordinat (jarak vertikal dari sumbu $x$ ).

Di ruang tiga dimensi, sebuah titik dinyatakan sebagai , dengan mewakili dimensi vertikal tambahan.

2. Jarak Antara Dua Titik

Rumus jarak antara dua titik dan dalam bidang dua dimensi adalah:

Rumus ini berasal dari teorema Pythagoras dan sangat berguna untuk menghitung panjang segmen garis yang menghubungkan dua titik di bidang kartesian.

3. Titik Tengah

Titik tengah antara dua titik dan dapat dihitung dengan rumus:

Titik ini merupakan titik yang membagi segmen garis yang menghubungkan $A$ dan $B$ menjadi dua bagian yang sama panjang.

4. Kemiringan Garis (Gradien)

Kemiringan (gradien) suatu garis adalah ukuran seberapa curam garis tersebut. Kemiringan garis yang melalui dua titik dan dihitung dengan rumus:

Gradien menunjukkan arah garis dan dapat digunakan untuk menentukan persamaan garis.

5. Persamaan Garis Lurus

Persamaan garis lurus dalam sistem koordinat kartesian dapat ditulis dalam beberapa bentuk, yang paling umum adalah:

Bentuk kemiringan-simpangan (slope-intercept form):

di mana $m$ adalah gradien dan $c$ adalah titik potong garis pada sumbu $y$ .

Bentuk umum:

di mana $A$ , $B$ , dan $C$ adalah konstanta.

6. Lingkaran

Persamaan lingkaran dalam sistem koordinat kartesian, dengan pusat di titik dan jari-jari $r$ , adalah:

Jika lingkaran berpusat di titik asal , maka persamaannya menjadi:

$x^{2} + y^{2} = r^{2}$

7. Parabola

Parabola adalah kurva yang berbentuk seperti huruf U. Persamaan parabola yang terbuka ke atas atau ke bawah adalah:

Sedangkan parabola yang terbuka ke kanan atau ke kiri memiliki persamaan:

8. Elips dan Hiperbola

Elips adalah kurva tertutup yang memiliki dua fokus. Persamaan umum elips adalah:
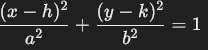
Hiperbola adalah kurva terbuka yang terdiri dari dua cabang. Persamaan umum hiperbola adalah:

Penerapan Geometri Analitik

Geometri analitik memiliki banyak penerapan dalam berbagai bidang, termasuk fisika, teknik, astronomi, dan bahkan ekonomi. Berikut beberapa contoh penerapannya:

1. Astronomi dan Navigasi

Dalam astronomi, geometri analitik digunakan untuk menghitung orbit planet dan benda langit lainnya. Dengan prinsip-prinsip geometri analitik, para ilmuwan dapat memprediksi posisi planet dan bintang di masa depan.

2. Rekayasa dan Desain

Insinyur menggunakan geometri analitik untuk merancang bangunan, jembatan, dan struktur lainnya. Persamaan geometris membantu dalam menghitung sudut, panjang, dan area yang dibutuhkan untuk konstruksi.

3. Grafik dalam Komputer

Dalam pemrograman komputer, geometri analitik digunakan untuk menggambar grafik dan gambar 3D. Prinsip-prinsip koordinat kartesian digunakan untuk memposisikan objek pada layar, baik dalam game maupun aplikasi desain grafis.

4. Fisik Partikel

Dalam fisika partikel, konsep seperti lintasan gerak partikel sering kali dianalisis menggunakan geometri analitik. Misalnya, lintasan proyektil atau gerak melingkar dapat diwakili dalam bentuk persamaan yang memudahkan analisis.

5. Ekonomi dan Statistik

Geometri analitik digunakan dalam ekonomi untuk memvisualisasikan data dan hubungan antara variabel. Grafik permintaan dan penawaran, serta kurva lainnya, dapat dianalisis menggunakan prinsip-prinsip geometri analitik.

FAQ Tentang Geometri Analitik

1. Apa yang dimaksud dengan sistem koordinat kartesian?

Sistem koordinat kartesian adalah sistem yang menggunakan dua sumbu (horizontal dan vertikal) untuk menentukan posisi titik di bidang dua dimensi.

2. Bagaimana persamaan garis lurus ditentukan?

Persamaan garis lurus ditentukan oleh gradien (kemiringan) dan titik potongnya pada sumbu $y$ . Bentuk umumnya adalah $y = m x + c$ , di mana $m$ adalah gradien dan $c$ adalah titik potong pada sumbu $y$ .

3. Apa perbedaan antara elips dan hiperbola?

Elips adalah kurva tertutup yang memiliki dua fokus, sedangkan hiperbola adalah kurva terbuka yang terdiri dari dua cabang dan juga memiliki dua fokus.

4. Bagaimana cara menghitung jarak antara dua titik?

Jarak antara dua titik dapat dihitung menggunakan rumus jarak:

5. Di mana geometri analitik diterapkan dalam kehidupan sehari-hari?

Geometri analitik diterapkan dalam banyak bidang seperti navigasi, arsitektur, desain grafis, astronomi, dan fisika.

Kesimpulan

Geometri analitik merupakan alat yang sangat berguna dalam matematika yang memungkinkan kita untuk menghubungkan konsep aljabar dengan geometri. Dengan menggunakan prinsip-prinsip koordinat kartesian, kita dapat menganalisis bentuk dan pola dalam berbagai situasi, mulai dari bangunan arsitektur hingga lintasan planet. Penerapan geometri analitik juga sangat luas, mencakup berbagai bidang ilmu dan teknologi.