Contoh Nyata tentang Pembagian Dua Fungsi dalam Kehidupan Sehari-Hari

Pembagian dua fungsi merupakan konsep matematika yang sering kali diaplikasikan dalam kehidupan sehari-hari, terutama dalam perhitungan yang melibatkan rasio atau efisiensi. Pembagian dua fungsi digunakan untuk membandingkan dua variabel atau mengukur seberapa besar satu variabel dapat dibagi oleh variabel lain dalam konteks tertentu. Salah satu contoh konkret dalam kehidupan sehari-hari adalah dalam menghitung kecepatan rata-rata, yaitu membagi jarak tempuh dengan waktu yang dibutuhkan untuk mencapai jarak tersebut. Contoh lain meliputi produktivitas kerja, efisiensi bahan bakar, hingga analisis biaya per unit produksi.

Berikut ini, kita akan membahas beberapa contoh nyata yang menerapkan konsep pembagian dua fungsi untuk mendapatkan informasi yang lebih rinci dan relevan dalam situasi sehari-hari.

Contoh 1: Menghitung Kecepatan Rata-Rata

Salah satu contoh paling umum dari pembagian dua fungsi adalah dalam perhitungan kecepatan rata-rata selama perjalanan. Jika seseorang mengemudi sejauh 150 kilometer dalam waktu 3 jam, kita dapat menggunakan pembagian dua fungsi untuk menghitung kecepatan rata-rata mereka.

Dalam kasus ini, kita memiliki dua fungsi:
1. Jarak Tempuh (J), yang merupakan fungsi dari tempat yang dilalui selama perjalanan.
2. Waktu Tempuh (T), yang merupakan fungsi dari lama waktu yang dibutuhkan untuk menempuh jarak tersebut.

Kecepatan rata-rata () dihitung dengan membagi jarak tempuh dengan waktu tempuh:

Di mana:

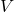• adalah kecepatan rata-rata dalam km/jam,
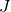• adalah jarak dalam kilometer,
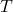• adalah waktu dalam jam.

Menggunakan contoh di atas, jika jarak tempuhnya 150 kilometer dan waktu tempuhnya 3 jam, maka:

Kecepatan rata-rata ini menunjukkan bahwa, secara keseluruhan, pengemudi tersebut bergerak dengan kecepatan rata-rata 50 km/jam. Perhitungan ini memberikan informasi yang penting untuk merencanakan perjalanan, mengukur efisiensi waktu, atau mengestimasi waktu kedatangan ke tujuan.

Contoh 2: Menghitung Efisiensi Bahan Bakar

Contoh lain dari pembagian dua fungsi adalah dalam perhitungan efisiensi bahan bakar kendaraan, yang mengukur seberapa jauh kendaraan dapat menempuh perjalanan dengan satu liter bahan bakar. Dalam hal ini, kita menggunakan dua variabel:
1. Jarak Tempuh (J) yang merupakan fungsi dari jarak yang ditempuh kendaraan,
2. Volume Bahan Bakar (B) yang merupakan fungsi dari jumlah bahan bakar yang digunakan.

Efisiensi bahan bakar () dihitung dengan membagi jarak tempuh dengan volume bahan bakar yang digunakan:

di mana:

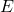• adalah efisiensi bahan bakar dalam km/liter,
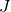• adalah jarak dalam kilometer,
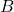• adalah volume bahan bakar dalam liter.

Misalkan, jika sebuah mobil menempuh jarak 300 km dengan 20 liter bensin, maka efisiensi bahan bakarnya adalah:

Nilai efisiensi bahan bakar ini menunjukkan bahwa mobil tersebut dapat menempuh 15 kilometer untuk setiap liter bensin. Informasi ini sangat bermanfaat bagi pemilik kendaraan dalam mengukur efisiensi penggunaan bahan bakar, yang kemudian dapat membantu dalam menghemat biaya bahan bakar dan merencanakan perjalanan jarak jauh.

Contoh 3: Produktivitas Kerja dalam Sebuah Proyek

Contoh pembagian dua fungsi lainnya adalah dalam mengukur produktivitas kerja suatu tim atau individu dalam proyek tertentu. Produktivitas sering kali dinyatakan sebagai jumlah output yang dihasilkan per satuan waktu kerja. Ini melibatkan dua variabel:
1. Jumlah Pekerjaan (P), yang merupakan fungsi dari pekerjaan atau output yang dihasilkan,
2. Waktu Kerja (W), yang merupakan fungsi dari waktu yang dibutuhkan untuk menyelesaikan pekerjaan.

Produktivitas () dihitung dengan membagi jumlah pekerjaan dengan waktu kerja:

di mana:

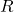• adalah produktivitas dalam unit output per jam,
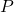• adalah jumlah pekerjaan atau output (misalnya, unit barang yang diproduksi),
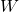• adalah waktu yang dibutuhkan dalam jam.

Sebagai contoh, jika sebuah tim produksi berhasil menyelesaikan 500 unit produk dalam waktu 25 jam, produktivitasnya dapat dihitung sebagai:

Produktivitas ini menunjukkan bahwa rata-rata, tim tersebut mampu menghasilkan 20 unit produk setiap jamnya. Informasi ini dapat berguna bagi perusahaan untuk mengukur efisiensi tim, mengidentifikasi kebutuhan peningkatan kinerja, serta menentukan target waktu penyelesaian pekerjaan berdasarkan produktivitas aktual.

Contoh 4: Biaya Produksi per Unit

Dalam dunia bisnis dan manufaktur, pembagian dua fungsi sering digunakan untuk menghitung biaya produksi per unit produk. Biaya produksi per unit penting untuk menentukan harga jual produk, mengukur efisiensi produksi, dan merencanakan anggaran. Dalam kasus ini, kita memiliki dua variabel utama:
1. Total Biaya Produksi (C), yang merupakan fungsi dari semua biaya yang dikeluarkan untuk menghasilkan produk,
2. Jumlah Produk (Q), yang merupakan fungsi dari jumlah produk yang dihasilkan.

Biaya produksi per unit () dihitung dengan membagi total biaya produksi dengan jumlah produk:

di mana:

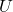• adalah biaya produksi per unit,
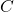• adalah total biaya produksi dalam rupiah,
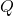• adalah jumlah produk yang dihasilkan.

Misalnya, jika sebuah pabrik mengeluarkan total biaya sebesar 100 juta rupiah untuk memproduksi 1.000 unit barang, maka biaya produksi per unitnya adalah:

Biaya produksi per unit ini memberikan informasi tentang biaya rata-rata untuk setiap unit yang dihasilkan. Informasi ini sangat penting dalam menentukan harga jual yang menguntungkan, mengelola biaya produksi, dan menganalisis apakah skala produksi sudah optimal atau perlu disesuaikan.

Contoh 5: Menghitung Biaya per Kilometer dalam Transportasi

Dalam industri transportasi, pembagian dua fungsi juga sangat bermanfaat, khususnya dalam menghitung biaya per kilometer untuk suatu perjalanan atau layanan transportasi. Ini berguna untuk perusahaan transportasi yang ingin menghitung tarif atau bagi individu yang ingin memperkirakan biaya perjalanan. Dalam kasus ini, dua variabel utama yang diperhitungkan adalah:
1. Total Biaya Transportasi (T), yang mencakup biaya bahan bakar, biaya perawatan kendaraan, dan lain-lain,
2. Jarak Tempuh (D), yang merupakan jarak total yang ditempuh dalam perjalanan.

Biaya per kilometer () dihitung dengan membagi total biaya transportasi dengan jarak tempuh:

di mana:

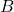• adalah biaya per kilometer,
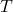• adalah total biaya dalam rupiah,
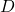• adalah jarak dalam kilometer.

Misalnya, jika total biaya perjalanan untuk sebuah kendaraan adalah 1 juta rupiah dengan jarak tempuh 500 kilometer, maka biaya per kilometer dapat dihitung sebagai:

Informasi biaya per kilometer ini sangat penting bagi perusahaan transportasi untuk menentukan tarif, serta bagi pengemudi individu untuk memperkirakan anggaran perjalanan yang lebih hemat dan sesuai kebutuhan.

Kesimpulan

Pembagian dua fungsi adalah konsep yang sangat berguna dalam berbagai situasi sehari-hari. Dalam contoh-contoh yang telah dibahas di atas, pembagian fungsi memungkinkan kita untuk menghitung kecepatan rata-rata, efisiensi bahan bakar, produktivitas kerja, biaya per unit produksi, dan biaya per kilometer dalam transportasi. Konsep ini memberikan wawasan penting tentang hubungan antar variabel dan membantu kita membuat perencanaan, keputusan, dan penyesuaian yang lebih baik dalam banyak aspek kehidupan dan bisnis.

Dengan memahami penerapan konsep pembagian dua fungsi, kita tidak hanya dapat memperoleh informasi yang relevan dan terukur, tetapi juga mengoptimalkan penggunaan sumber daya, meningkatkan efisiensi, dan merencanakan tindakan yang lebih tepat sasaran dalam berbagai konteks kehidupan sehari-hari.