Dalam matematika, perkalian fungsi merupakan salah satu konsep penting yang sering diaplikasikan dalam kehidupan sehari-hari. Perkalian dua fungsi berarti mengalikan nilai dari dua fungsi berbeda pada domain yang sama untuk mendapatkan fungsi baru. Contoh penerapannya dapat ditemukan dalam berbagai bidang, seperti ekonomi, fisika, dan teknik, yang semuanya memanfaatkan konsep ini untuk memecahkan masalah-masalah kompleks. Salah satu contoh konkret perkalian dua fungsi dalam kehidupan sehari-hari adalah dalam perhitungan konsumsi energi rumah tangga berdasarkan penggunaan perangkat listrik dan tarif listrik.
Perkalian Dua Fungsi dalam Menghitung Konsumsi Energi Listrik Rumah Tangga
Mari kita ambil contoh rumah tangga yang ingin mengetahui biaya listrik yang harus dibayarkan setiap bulan. Dalam kasus ini, ada dua faktor utama yang berkontribusi terhadap biaya listrik, yaitu jumlah energi yang digunakan setiap perangkat listrik dan tarif per kWh (kilowatt-hour) yang dikenakan oleh perusahaan listrik. Kedua faktor ini masing-masing dapat diekspresikan sebagai fungsi. Ketika kita mengalikan kedua fungsi ini, kita dapat menentukan total biaya listrik bulanan.
1. Fungsi Konsumsi Energi
Fungsi pertama adalah fungsi yang menggambarkan konsumsi energi masing-masing perangkat listrik di rumah. Misalkan kita memiliki beberapa perangkat listrik seperti kulkas, AC, lampu, dan mesin cuci. Setiap perangkat ini memiliki kebutuhan daya dalam kilowatt (kW) dan durasi pemakaian dalam jam (h) yang berbeda. Konsumsi energi dari suatu perangkat dapat dihitung dengan mengalikan daya perangkat (dalam kW) dengan jumlah waktu pemakaian (dalam jam). Maka fungsi konsumsi energi perangkat listrik 
dalam satu bulan adalah:
![\[ E(t) = P \times t \]](https://sridianti.com/wp-content/uploads/2024/11/quicklatex.com-a228e22f0d42823a8a43d9212bb9b6f9_l3.png "Rendered by QuickLaTeX.com")
di mana:
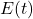- adalah energi yang dikonsumsi dalam kWh,
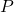adalah daya perangkat dalam kW,
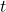adalah waktu pemakaian perangkat dalam jam per bulan.
Contohnya, jika sebuah AC memiliki daya 1,5 kW dan digunakan selama 5 jam sehari, maka konsumsi energi bulanan perangkat tersebut adalah:
![\[ E_{AC} = 1,5 \, \text{kW} \times (5 \, \text{jam/hari} \times 30 \, \text{hari}) = 1,5 \times 150 = 225 \, \text{kWh} \]](https://sridianti.com/wp-content/uploads/2024/11/quicklatex.com-0a4846292914984b35e1dacbe0f6575b_l3.png "Rendered by QuickLaTeX.com")
Dengan cara yang sama, konsumsi energi bulanan dari perangkat lain dapat dihitung sesuai dengan daya dan durasi pemakaiannya. Fungsi ini memberikan gambaran tentang total energi yang dikonsumsi oleh perangkat dalam satu bulan.
2. Fungsi Tarif Listrik
Fungsi kedua yang perlu diperhatikan adalah fungsi tarif listrik yang dikenakan oleh perusahaan listrik. Tarif listrik biasanya ditentukan per kWh dan dapat bervariasi berdasarkan tingkatan konsumsi. Misalkan tarif dasar listrik adalah 1.500 rupiah per kWh untuk penggunaan rumah tangga. Maka fungsi tarif listrik, 
, adalah:
![\[ T(E) = 1.500 \times E \]](https://sridianti.com/wp-content/uploads/2024/11/quicklatex.com-f9d868666f59a84b9399075352d1bb12_l3.png "Rendered by QuickLaTeX.com")
di mana:
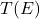- adalah total biaya dalam rupiah,
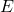adalah energi yang digunakan dalam kWh.
Fungsi tarif ini akan kita gunakan untuk mengalikan total konsumsi energi rumah tangga (hasil dari fungsi pertama) guna memperoleh biaya listrik yang harus dibayar.
Menggabungkan Kedua Fungsi: Perkalian Fungsi Konsumsi Energi dan Tarif
Setelah kita memiliki kedua fungsi tersebut, kita dapat mengalikan hasil dari fungsi konsumsi energi dan fungsi tarif listrik untuk mendapatkan biaya listrik total. Proses ini adalah contoh perkalian dua fungsi yang sangat relevan dalam kehidupan sehari-hari. Kita menggabungkan dua fungsi dengan cara perkalian untuk mengetahui biaya yang harus dibayarkan.
Misalkan, untuk seluruh perangkat listrik di rumah, total konsumsi energi bulanan adalah 500 kWh. Dengan tarif 1.500 rupiah per kWh, total biaya listrik 
dapat dihitung dengan mengalikan kedua fungsi tersebut:
![\[ C = T(E) \times E(t) = 1.500 \times 500 = 750.000 \, \text{rupiah} \]](https://sridianti.com/wp-content/uploads/2024/11/quicklatex.com-84c9940e4f9641fe8f0f44f96c28b1ee_l3.png "Rendered by QuickLaTeX.com")
Ini adalah hasil dari perkalian dua fungsi yang berbeda: fungsi konsumsi energi dan fungsi tarif listrik . Dengan cara ini, kita mendapatkan total biaya listrik bulanan, yang mencerminkan beban biaya yang harus dikeluarkan untuk konsumsi energi rumah tangga.
Aplikasi Lanjutan: Menghemat Biaya Listrik melalui Perkalian Fungsi
Setelah memahami perkalian kedua fungsi ini, kita dapat menggunakannya untuk mencari cara menghemat biaya listrik dengan memodifikasi salah satu fungsi. Misalnya, kita dapat menurunkan fungsi konsumsi energi dengan mengurangi waktu pemakaian atau menggunakan perangkat yang lebih hemat energi. Ini akan menurunkan nilai , yang pada gilirannya menurunkan hasil perkalian dengan tarif listrik, sehingga total biaya listrik yang dihasilkan menjadi lebih kecil.
Jika rumah tangga mengganti perangkat yang lebih hemat energi atau mengurangi waktu pemakaian AC menjadi 3 jam per hari (dari sebelumnya 5 jam per hari), maka konsumsi energi AC dalam sebulan berubah menjadi:
![\[ E_{AC} = 1,5 \times (3 \times 30) = 1,5 \times 90 = 135 \, \text{kWh} \]](https://sridianti.com/wp-content/uploads/2024/11/quicklatex.com-e3551aa8d59c75359cf6170e77fb108b_l3.png "Rendered by QuickLaTeX.com")
Jika seluruh perangkat lainnya tetap digunakan seperti biasa, dan total konsumsi energi rumah tangga menjadi 400 kWh, maka total biaya yang harus dibayarkan dengan tarif 1.500 rupiah per kWh adalah:
![\[ C = 1.500 \times 400 = 600.000 \, \text{rupiah} \]](https://sridianti.com/wp-content/uploads/2024/11/quicklatex.com-6a0a5b24941369a8c825f3d2426ce1cc_l3.png "Rendered by QuickLaTeX.com")
Perkalian fungsi dalam contoh ini membantu dalam menunjukkan bahwa dengan mengurangi waktu pemakaian atau memilih perangkat hemat energi, biaya listrik yang harus dibayar bisa dikurangi. Ini memberikan gambaran yang jelas tentang bagaimana pengaruh masing-masing variabel dalam perkalian fungsi terhadap hasil akhir dan bagaimana rumah tangga dapat mengontrol biaya melalui pengelolaan konsumsi energi.
Konsep Perkalian Fungsi dalam Situasi Lain
Selain dalam perhitungan biaya listrik, perkalian dua fungsi ini juga diterapkan dalam banyak situasi lain dalam kehidupan sehari-hari. Misalnya, dalam bidang ekonomi, untuk menghitung total pendapatan suatu usaha kecil yang menjual produk.
Misalkan:
- Fungsi pertama,
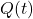, menyatakan jumlah produk yang terjual dalam suatu periode tertentu (misalnya, jumlah produk per minggu atau per bulan). - Fungsi kedua,
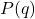, menyatakan harga per unit produk.
Dengan mengalikan kedua fungsi ini, total pendapatan 
dari penjualan produk dalam periode tertentu dapat dihitung sebagai:
![\[ R = P(q) \times Q(t) \]](https://sridianti.com/wp-content/uploads/2024/11/quicklatex.com-5766e1c65f9358a93ad91457b13864a8_l3.png "Rendered by QuickLaTeX.com")
Jika sebuah usaha menjual 100 produk per bulan dengan harga 50.000 rupiah per produk, total pendapatan dari penjualan tersebut adalah:
![\[ R = 50.000 \times 100 = 5.000.000 \, \text{rupiah} \]](https://sridianti.com/wp-content/uploads/2024/11/quicklatex.com-e9c60630d11984e83aedeaf3afa92800_l3.png "Rendered by QuickLaTeX.com")
Perkalian fungsi penjualan dan harga satuan produk ini memberikan informasi tentang total pendapatan yang diperoleh. Dengan mengetahui ini, pemilik usaha bisa memperkirakan pendapatan bulanan mereka dan merencanakan strategi bisnis berdasarkan target penjualan dan harga jual produk.
Kesimpulan
Perkalian dua fungsi dalam kehidupan sehari-hari merupakan konsep yang sangat praktis dan sering digunakan dalam berbagai situasi nyata. Contoh penghitungan biaya listrik rumah tangga berdasarkan konsumsi energi dan tarif per kWh menunjukkan bagaimana perkalian fungsi membantu dalam menghitung total biaya yang harus dibayar, sementara contoh dalam bidang ekonomi menunjukkan bagaimana total pendapatan dapat dihitung melalui perkalian antara jumlah produk terjual dan harga per unit produk.
Dengan memahami perkalian fungsi, kita dapat menerapkan konsep ini untuk membuat keputusan yang lebih cerdas dalam manajemen keuangan dan operasional, baik dalam rumah tangga maupun bisnis. Konsep ini juga membantu kita memahami bagaimana berbagai faktor dalam suatu sistem saling berkaitan dan berdampak pada hasil akhir, memberikan wawasan yang lebih mendalam untuk pengambilan keputusan yang lebih efektif.
