Contoh Situasi dalam Kehidupan Sehari-Hari di Mana Domain Fungsi Tidak Dapat Bernilai Negatif

Dalam kehidupan sehari-hari, konsep domain fungsi yang tidak bisa bernilai negatif sering kali ditemui dalam berbagai situasi praktis. Salah satu contohnya adalah dalam konteks mengukur jumlah waktu yang berlalu sejak suatu kejadian terjadi atau menghitung volume suatu objek yang diproduksi. Mari kita eksplorasi contoh konkret dalam kasus praktis yang sederhana namun sangat relevan dengan kehidupan kita: mengukur jumlah bahan bakar dalam tangki kendaraan.

Mengukur Jumlah Bahan Bakar dalam Tangki Kendaraan

Pertimbangkan situasi ketika seseorang ingin mengetahui jumlah bahan bakar dalam tangki mobilnya dari waktu ke waktu, khususnya saat melakukan perjalanan panjang. Fungsi yang mengukur jumlah bahan bakar ini bergantung pada berapa banyak bahan bakar yang digunakan selama perjalanan. Untuk situasi ini, mari kita anggap fungsi mewakili jumlah bahan bakar di tangki mobil pada waktu tertentu .

Mengapa Domain Fungsi Tidak Dapat Bernilai Negatif?

Dalam fungsi , waktu selalu bernilai positif atau nol, dimulai dari saat perjalanan dimulai (ketika ). Hal ini terjadi karena waktu secara alami hanya mengalir maju, dan tidak masuk akal untuk memiliki waktu yang bernilai negatif dalam situasi ini. Selain itu, jumlah bahan bakar dalam tangki mobil juga tidak bisa bernilai negatif. Kita mungkin memiliki jumlah bahan bakar yang mendekati nol, tetapi dalam kehidupan nyata, tidak akan ada situasi di mana jumlah bahan bakar di tangki menjadi negatif. Jika bensin habis, maka sama dengan nol, bukan negatif.

Dalam contoh ini, domain fungsi hanya mencakup nilai-nilai waktu yang positif (atau nol) karena waktu negatif tidak relevan dalam konteks perjalanan yang baru saja dimulai. Dengan kata lain, waktu dimulai dari 0 (saat berangkat) dan hanya bisa bertambah seiring perjalanan berlangsung.

Mengapa Fungsi Tidak Mungkin Bernilai Negatif?

Selain domain waktu yang tidak bisa bernilai negatif, fungsi yang mengukur jumlah bahan bakar di tangki pun tidak bisa memiliki nilai negatif. Dalam dunia nyata, jumlah bahan bakar merupakan kuantitas fisik yang tidak mungkin lebih kecil dari nol. Bahkan ketika tangki bahan bakar kosong sepenuhnya, nilai menjadi nol, bukan negatif.

Penggunaan Fungsi dalam Penghitungan Bahan Bakar Selama Perjalanan

Misalkan fungsi mewakili jumlah bahan bakar dalam tangki mobil pada waktu tertentu . Dalam praktiknya, fungsi ini akan menurun seiring bertambahnya waktu jika mobil terus berjalan. Fungsi ini bisa dirumuskan sebagai:

di mana:

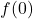• adalah jumlah bahan bakar awal di tangki (dalam liter) ketika perjalanan dimulai,
• adalah laju penggunaan bahan bakar kendaraan (misalnya, liter per jam),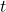
• adalah waktu yang telah berlalu sejak perjalanan dimulai (dalam jam).

Karena fungsi ini mewakili jumlah bahan bakar di tangki, domain dari hanya mencakup nilai positif atau nol. Saat waktu meningkat, berkurang sesuai dengan laju konsumsi bahan bakar . Dengan kata lain, bahan bakar dalam tangki akan berkurang hingga mendekati nol. Namun, tidak mungkin fungsi ini menghasilkan nilai negatif, karena jumlah bahan bakar tidak mungkin kurang dari nol.

Jika, misalnya, jumlah bahan bakar awal adalah 50 liter dan laju penggunaan bahan bakar adalah 5 liter per jam, maka fungsi menjadi:

Pada saat , jumlah bahan bakar adalah 50 liter. Setelah 5 jam perjalanan (), jumlah bahan bakar tersisa adalah:

Setelah 10 jam perjalanan, jumlah bahan bakar akan menjadi:

Setelah 10 jam, bahan bakar habis, tetapi jumlah bahan bakar tetap nol tanpa pernah menjadi negatif.

Menghindari Kesalahan Interpretasi dengan Domain Positif

Menggunakan fungsi dengan domain waktu dan bahan bakar yang selalu positif (atau nol) membantu dalam memahami batasan nyata yang ada dalam kehidupan sehari-hari. Jika kita salah memasukkan nilai negatif pada fungsi , hasilnya akan menjadi tidak logis. Misalnya, jika kita menggunakan nilai waktu negatif, seperti , fungsi akan menjadi:

Hasil ini tidak realistis karena jumlah bahan bakar tidak bisa bertambah hanya karena waktu berjalan mundur. Secara fisik, jumlah bahan bakar di tangki pada awal perjalanan ditentukan saat dan hanya dapat berkurang dengan perjalanan waktu positif.

Pentingnya Memahami Domain Positif dalam Aplikasi Kehidupan Sehari-Hari

Dalam situasi lain, seperti mengukur jumlah uang di rekening tabungan atau jumlah produk dalam stok, domain fungsi juga sering kali terbatas pada nilai positif. Dengan demikian, memahami bahwa domain fungsi tertentu tidak dapat bernilai negatif adalah penting untuk memastikan keakuratan hasil penghitungan dan menghindari interpretasi yang tidak realistis.

Dalam kasus bahan bakar, waktu dan kuantitas bahan bakar merupakan variabel yang hanya memiliki arti dalam domain positif. Kesalahan dalam memasukkan nilai negatif untuk variabel-variabel ini dapat memberikan hasil yang tidak sesuai dengan kenyataan, bahkan bisa menyebabkan kesalahan serius dalam perencanaan perjalanan atau penghitungan konsumsi.

Kesimpulan

Mengukur bahan bakar dalam tangki kendaraan adalah contoh yang sangat sederhana namun jelas tentang mengapa domain fungsi dalam beberapa kasus tidak dapat bernilai negatif. Waktu yang selalu berjalan maju dan kuantitas bahan bakar yang tidak mungkin negatif menunjukkan pentingnya memilih domain fungsi yang sesuai. Dengan memahami hal ini, kita dapat menghindari kesalahan interpretasi dan mendapatkan pemahaman yang lebih tepat mengenai penggunaan fungsi dalam kehidupan sehari-hari.