Dalam setiap eksperimen atau pengukuran, kita tidak pernah bisa mendapatkan hasil yang benar-benar pasti. Selalu ada ketidakpastian yang menyertai hasil pengukuran, baik karena keterbatasan alat ukur, kondisi pengukuran, maupun faktor manusia. Memahami dan memperhitungkan ketidakpastian pengukuran sangat penting untuk mendapatkan hasil yang akurat dan dapat diandalkan. Artikel ini akan membahas konsep ketidakpastian pengukuran, jenis-jenis ketidakpastian, serta beberapa metode untuk menghitungnya.
1. Apa Itu Ketidakpastian Pengukuran?
Ketidakpastian pengukuran adalah parameter yang mencerminkan seberapa jauh hasil pengukuran bisa menyimpang dari nilai sebenarnya. Ketidakpastian bukanlah kesalahan, melainkan batas yang menunjukkan kemungkinan variasi hasil pengukuran. Dengan kata lain, ketidakpastian memberikan rentang di mana nilai sebenarnya dari pengukuran diperkirakan berada.
Sebagai contoh, jika kita mengukur panjang sebuah benda dan mendapatkan hasil ![]() , maka kita memperkirakan bahwa panjang sebenarnya berada di antara
, maka kita memperkirakan bahwa panjang sebenarnya berada di antara ![]() dan
dan ![]() .
.
Mengapa Ketidakpastian Penting?
Ketidakpastian pengukuran penting karena:
- Menggambarkan keandalan hasil pengukuran.
- Memungkinkan komparasi antara hasil pengukuran yang berbeda.
- Mencegah kesalahan interpretasi ketika hasil pengukuran digunakan untuk tujuan ilmiah atau praktis.
2. Jenis-Jenis Ketidakpastian Pengukuran
Ada dua jenis utama ketidakpastian pengukuran berdasarkan sumbernya: ketidakpastian acak dan ketidakpastian sistematis.
a. Ketidakpastian Acak (Random Uncertainty)
Ketidakpastian acak muncul dari variabilitas tak terduga dalam proses pengukuran. Ini bisa disebabkan oleh faktor-faktor seperti perubahan lingkungan, fluktuasi alat ukur, atau keterbatasan manusia dalam membaca hasil pengukuran.
Ciri-ciri ketidakpastian acak:
- Dapat terjadi baik dalam pengukuran tunggal maupun pengukuran berulang.
- Cenderung menyebabkan hasil pengukuran tersebar di sekitar nilai rata-rata secara acak.
- Dapat dikurangi dengan melakukan pengukuran berulang dan mengambil nilai rata-rata.
Contoh: Saat mengukur panjang dengan penggaris, hasil pengukuran mungkin sedikit berbeda setiap kali karena variasi dalam cara membaca skala penggaris.
b. Ketidakpastian Sistematis (Systematic Uncertainty)
Ketidakpastian sistematis adalah penyimpangan yang terjadi secara konsisten dalam arah yang sama (lebih besar atau lebih kecil) dari nilai sebenarnya. Ini biasanya disebabkan oleh kesalahan dalam alat ukur atau metode pengukuran yang digunakan.
Ciri-ciri ketidakpastian sistematis:
- Tidak dapat dikurangi dengan pengukuran berulang.
- Dapat menyebabkan bias pada hasil pengukuran.
- Harus diidentifikasi dan dikoreksi, misalnya dengan mengkalibrasi alat ukur.
Contoh: Jika termometer yang digunakan untuk mengukur suhu selalu menunjukkan hasil 2°C lebih tinggi karena kalibrasi yang salah, maka ini adalah ketidakpastian sistematis.
3. Cara Menghitung Ketidakpastian Pengukuran
Untuk menghitung ketidakpastian pengukuran, kita perlu mempertimbangkan beberapa hal, seperti seberapa sering pengukuran dilakukan (pengukuran tunggal atau berulang), jenis alat yang digunakan, serta metode pengukuran yang diterapkan.
a. Ketidakpastian Pengukuran Tunggal
Dalam pengukuran tunggal, ketidakpastian biasanya ditentukan berdasarkan resolusi alat ukur atau toleransi dari alat tersebut.
- Resolusi alat ukur: Ketidakpastian minimal dari alat ukur ditentukan oleh skala terkecil yang bisa dibaca dari alat tersebut. Misalnya, jika kita menggunakan penggaris dengan skala terkecil 1 mm, maka ketidakpastian pengukuran bisa dianggap
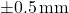 .
. - Toleransi alat ukur: Beberapa alat ukur memiliki toleransi yang dinyatakan oleh pabrik pembuat. Misalnya, sebuah voltmeter mungkin memiliki ketidakpastian
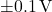 untuk setiap pengukuran.
untuk setiap pengukuran.
Penjumlahan atau Pengurangan dengan Ketidakpastian Pengukuran Tunggal
Ketika kita melakukan operasi penjumlahan atau pengurangan pada pengukuran yang memiliki ketidakpastian, aturan dasarnya adalah bahwa ketidakpastian absolut dari masing-masing pengukuran harus ditambahkan.
Aturan Dasar:
Jika kita memiliki dua pengukuran tunggal ![]() dan
dan ![]() , maka:
, maka:
- Penjumlahan:
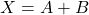
- Pengurangan:
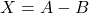
Untuk ketidakpastiannya:
![]()
Ketidakpastian total ![]() adalah penjumlahan langsung dari ketidakpastian absolut masing-masing pengukuran. Ini berlaku baik untuk operasi penjumlahan maupun pengurangan.
adalah penjumlahan langsung dari ketidakpastian absolut masing-masing pengukuran. Ini berlaku baik untuk operasi penjumlahan maupun pengurangan.
Contoh Penjumlahan:
Misalkan kita ingin menjumlahkan dua panjang batang:
- Batang pertama:
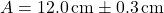
- Batang kedua:
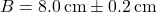
Jika kita menjumlahkan kedua panjang tersebut:
![]()
Ketidakpastian totalnya adalah:
![]()
Jadi, hasil akhirnya adalah:
![]()
Contoh Pengurangan:
Jika kita ingin menghitung selisih panjang dua batang:
![]()
Ketidakpastian totalnya tetap dijumlahkan secara langsung:
![]()
Jadi, hasil akhirnya adalah:
![]()
- —
Perkalian atau Pembagian dengan Ketidakpastian Pengukuran Tunggal
Untuk perkalian dan pembagian pengukuran tunggal, kita perlu memperhitungkan ketidakpastian relatif (yaitu ketidakpastian dalam bentuk persentase atau fraksi dari nilai yang diukur).
Aturan Dasar:
Jika kita memiliki dua pengukuran tunggal ![]() dan
dan ![]() , maka:
, maka:
- Perkalian:
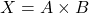
- Pembagian:
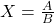
Untuk ketidakpastiannya:
![]()
Ketidakpastian relatif ![]() adalah penjumlahan langsung dari ketidakpastian relatif masing-masing pengukuran. Ketidakpastian absolut
adalah penjumlahan langsung dari ketidakpastian relatif masing-masing pengukuran. Ketidakpastian absolut ![]() dapat diperoleh dengan mengalikan ketidakpastian relatif tersebut dengan hasil perkalian atau pembagian
dapat diperoleh dengan mengalikan ketidakpastian relatif tersebut dengan hasil perkalian atau pembagian ![]() .
.
Contoh Perkalian:
Misalkan kita ingin menghitung luas sebuah persegi panjang dengan panjang dan lebar berikut:
- Panjang:
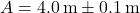
- Lebar:
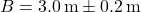
Luas persegi panjang adalah:
![]()
Untuk menghitung ketidakpastian, kita hitung ketidakpastian relatif terlebih dahulu:
![]()
![]()
Ketidakpastian relatif dari ![]() adalah:
adalah:
![]()
Ketidakpastian absolut ![]() adalah:
adalah:
![]()
Jadi, hasil akhirnya adalah:
![]()
Contoh Pembagian:
Misalkan kita ingin menghitung kecepatan rata-rata sebuah mobil yang menempuh jarak ![]() dalam waktu
dalam waktu ![]() :
:
- Jarak:
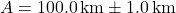
- Waktu:
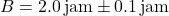
Kecepatan rata-rata adalah:
![]()
Untuk menghitung ketidakpastian relatif:
![]()
![]()
Ketidakpastian relatif dari ![]() adalah:
adalah:
![]()
Ketidakpastian absolut ![]() adalah:
adalah:
![]()
Jadi, hasil akhirnya adalah:
![]()
b. Ketidakpastian Pengukuran Berulang
Jika pengukuran dilakukan beberapa kali, kita bisa menggunakan statistik dasar untuk menghitung ketidakpastian. Langkah-langkah perhitungannya adalah sebagai berikut:
1. Hitung rata-rata pengukuran:
Misalkan kita melakukan ![]() kali pengukuran dengan hasil
kali pengukuran dengan hasil ![]() , maka rata-rata pengukuran
, maka rata-rata pengukuran ![]() adalah:
adalah:
![]()
2. Hitung simpangan baku (standard deviation):
Simpangan baku ![]() menunjukkan seberapa jauh hasil pengukuran tersebar dari rata-ratanya. Rumusnya adalah:
menunjukkan seberapa jauh hasil pengukuran tersebar dari rata-ratanya. Rumusnya adalah:
![Rendered by QuickLaTeX.com \[ \sigma = \sqrt{\frac{\sum_{i=1}^{n} (X_i - \bar{X})^2}{n - 1}} \]](https://sridianti.com/wp-content/uploads/2024/11/quicklatex.com-84dd47872545e78c2a106bf93353698a_l3.png)
3. Hitung simpangan baku rata-rata (standard deviation of the mean):
Ketidakpastian rata-rata pengukuran dapat dihitung menggunakan simpangan baku rata-rata, yang didefinisikan sebagai:
![]()
Dengan ini, kita bisa menyatakan hasil pengukuran sebagai ![]() .
.
Penjumlahan dan Pengurangan Pengukuran Berulang
Ketika kita menjumlahkan atau mengurangi dua besaran fisik yang diukur berulang kali, kita juga harus memperhitungkan ketidakpastian dari hasil pengukuran tersebut.
Aturan Penjumlahan dan Pengurangan Ketidakpastian Pengukuran Berulang:
Jika kita memiliki dua hasil pengukuran rata-rata ![]() dan
dan ![]() , maka:
, maka:
- Penjumlahan:
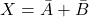
- Pengurangan:
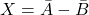
Untuk ketidakpastiannya:
![]()
Ketidakpastian total ![]() dihitung dengan menjumlahkan kuadrat dari ketidakpastian pengukuran rata-rata, lalu mengambil akar kuadrat dari hasil tersebut.
dihitung dengan menjumlahkan kuadrat dari ketidakpastian pengukuran rata-rata, lalu mengambil akar kuadrat dari hasil tersebut.
Contoh Penjumlahan Pengukuran Berulang:
Misalkan kita mengukur panjang dua batang kayu secara berulang:
- Batang pertama:
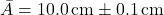
- Batang kedua:
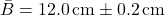
Jika kita ingin menjumlahkan kedua panjang tersebut:
![]()
Ketidakpastian totalnya:
![]()
Jadi, hasil akhirnya adalah:
![]()
Contoh Pengurangan Pengukuran Berulang:
Misalkan kita ingin menghitung selisih panjang kedua batang:
![]()
Ketidakpastian total tetap sama:
![]()
Jadi, hasil akhirnya adalah:
![]()
- —
Perkalian dan Pembagian Pengukuran Berulang
Untuk perkalian dan pembagian pengukuran berulang, ketidakpastian relatif digunakan untuk menghitung ketidakpastian total dari hasil operasi tersebut.
Aturan Perkalian dan Pembagian Ketidakpastian Pengukuran Berulang:
Jika kita memiliki dua hasil pengukuran rata-rata ![]() dan
dan ![]() , maka:
, maka:
- Perkalian:
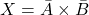
- Pembagian:
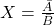
Untuk ketidakpastiannya:
![Rendered by QuickLaTeX.com \[ \frac{\Delta X}{X} = \sqrt{\left( \frac{\Delta \bar{A}}{\bar{A}} \right)^2 + \left( \frac{\Delta \bar{B}}{\bar{B}} \right)^2} \]](https://sridianti.com/wp-content/uploads/2024/11/quicklatex.com-c70ca2b0f5af141779b83697ff4e98ac_l3.png)
Ketidakpastian relatif ![]() dihitung dengan menjumlahkan kuadrat dari ketidakpastian relatif masing-masing pengukuran rata-rata, lalu mengambil akar kuadrat dari hasil tersebut. Ketidakpastian absolut dari
dihitung dengan menjumlahkan kuadrat dari ketidakpastian relatif masing-masing pengukuran rata-rata, lalu mengambil akar kuadrat dari hasil tersebut. Ketidakpastian absolut dari ![]() kemudian diperoleh dengan mengalikan ketidakpastian relatif tersebut dengan hasil operasi.
kemudian diperoleh dengan mengalikan ketidakpastian relatif tersebut dengan hasil operasi.
Contoh Perkalian Pengukuran Berulang:
Misalkan kita ingin menghitung luas sebuah persegi panjang berdasarkan pengukuran berulang panjang dan lebarnya:
- Panjang:
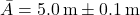
- Lebar:
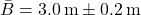
Luas persegi panjang adalah:
![]()
Ketidakpastian relatifnya:
![]()
![]()
Ketidakpastian relatif dari ![]() :
:
![]()
Ketidakpastian absolut dari ![]() :
:
![]()
Jadi, hasil akhirnya adalah:
![]()
Contoh Pembagian Pengukuran Berulang:
Misalkan kita ingin menghitung kecepatan rata-rata berdasarkan pengukuran berulang jarak dan waktu:
- Jarak:
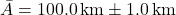
- Waktu:
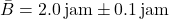
Kecepatan rata-rata adalah:
![]()
Ketidakpastian relatifnya:
![]()
![]()
Ketidakpastian relatif dari ![]() :
:
![]()
Ketidakpastian absolut dari ![]() :
:
![]()
Jadi, hasil akhirnya adalah:
![]()
- —
c. Ketidakpastian Kombinasi
Dalam banyak kasus, hasil akhir eksperimen melibatkan beberapa pengukuran. Oleh karena itu, kita perlu menghitung ketidakpastian kombinasi ketika kita melakukan operasi matematika, seperti penjumlahan, pengurangan, perkalian, atau pembagian, pada beberapa pengukuran yang memiliki ketidakpastian.
Penjumlahan atau Pengurangan:
Jika kita memiliki dua pengukuran ![]() dan
dan ![]() , maka ketidakpastian totalnya adalah:
, maka ketidakpastian totalnya adalah:
![]()
Perkalian atau Pembagian:
Jika kita memiliki dua pengukuran ![]() dan
dan ![]() , maka ketidakpastian relatifnya dihitung sebagai:
, maka ketidakpastian relatifnya dihitung sebagai:
![Rendered by QuickLaTeX.com \[ \frac{\Delta X}{X} = \sqrt{\left( \frac{\Delta A}{A} \right)^2 + \left( \frac{\Delta B}{B} \right)^2} \]](https://sridianti.com/wp-content/uploads/2024/11/quicklatex.com-b5ebde28d0f1270ae93ff336ccde62a5_l3.png)
4. Penyajian Hasil Pengukuran dengan Ketidakpastian
Setelah menghitung ketidakpastian, hasil pengukuran harus disajikan dengan cara yang jelas dan konsisten. Beberapa aturan umum yang perlu diperhatikan:
1. Angka penting: Ketidakpastian sebaiknya dinyatakan dengan satu angka penting, dan hasil pengukuran harus dibulatkan sesuai dengan ketidakpastiannya. Misalnya, jika hasil pengukuran adalah ![]() , maka kita bisa menuliskannya sebagai
, maka kita bisa menuliskannya sebagai ![]() .
.
2. Satuan yang konsisten: Pastikan bahwa hasil pengukuran dan ketidakpastiannya menggunakan satuan yang sama.
5. Kesimpulan
Ketidakpastian pengukuran adalah aspek penting dalam setiap eksperimen ilmiah. Memahami dan menghitung ketidakpastian dengan benar memastikan bahwa hasil pengukuran dapat diinterpretasikan dengan akurat dan dapat dibandingkan dengan hasil eksperimen lainnya. Ada dua jenis ketidakpastian, yakni acak dan sistematis, yang keduanya harus diperhitungkan untuk mendapatkan hasil yang reliabel. Baik dalam pengukuran tunggal maupun berulang, ada metode statistik yang dapat digunakan untuk menghitung ketidakpastian, serta cara yang tepat untuk menyajikan hasil pengukuran tersebut.
Dengan penerapan yang baik, kita dapat membuat kesimpulan yang lebih akurat dan mengurangi kemungkinan kesalahan dalam eksperimen atau analisis data lebih lanjut.